Квантовая механика предсказывает, что измерения на пространственно разделенных частицах могут давать нелокальные
корреляции.
Это твёрдо установлено на опыте, но нелегко поддаётся интуитивным представлениям о пространстве и времени.
Концепция "управления" (steering) помогает понять квантовую нелокальность.
Истолкование квантовой механики привлекает внимание
самых выдающихся физиков без малого целый век.
Несмотря на все усилия, глубокое интуитивное понимание теории до сих пор не достигнуто.
Среди всех особенностей квантовой механики, возможно, самый
ярких пример, - это квантовая нелокальность: пространственно
разделенные квантовые частицы могут вести себя так, что цельность нашего восприятия
пространства и времени нарушается.
Квантовая нелокальность является также ключевым элементом в
перспективных приложениях в области
обработки информации (квантовый компьютер).
Недавно Саундерс и др. [1] предложили свежий
взгляд на квантовую нелокальность, исследовав малоизученную концепцию "управления" (steering).
Термин steering ввел Шрёдингер [2] для обозначения управления редукцией волнового пакета на расстоянии.
Локальность - очень естественный физический принцип.
В нашем повседневном опыте все объекты находятся под влиянием непосредственно только
их непосредственного окружения, а не удаленных объектов.
Любое воздействие на расстоянии передаётся каким-нибудь физическим полем, например,
электромагнитным, которое родившись в одном месте, действует на предметы в другом месте.
Все эти процессы (рождения и поглощения полей) локальны.
Не так обстоит дело в квантовой механике: квантовые частицы могут иметь подлинно нелокальные
корреляции, т.е. "чувствовать" друг друга на огромных расстояниях.
Представим себе двух пространственно
разделённых экспериментаторов, Алю и Борю, которые изучают пару "запутанных" фотонов, т.е.
таких, которые родились совместно, и какие-то квантовые числа их исходного состояния (например, суммарный импульс,
или суммарный момент импульса) заданы.
Квантовая теория предсказывает, что независимо от того, как далеко друг от друга находятся Аля и Боря, их
фотоны будут вести себя как один физический объект: если Аля делает измерение для своего фотона,
состояние парного фотона Бори будет изменено мгновенно.
До измерения Алей ни импульс, ни момент её фотона не известен.
Измерит Аля импульс - мгновенно становится известен импульс Бориного фотона (путём вычитания из суммарного
импульса Алиного значения).
Измерит Аля момент - результат Бориного измерения момента его фотона тут же становится предопределён.
Опять же мгновенно, причём, если Аля и Боря разделены расстоянием в несколько световых лет,
Боря не узнает об Алином измерении несколько лет, пока её сообщение до него не дойдёт.
Такое утверждение кажется столь поразительно нелогичным, что
можно усомниться - как и сделали
Альберт Эйнштейн, Борис Подольский и Натан Розен [3] - имеет ли это предсказание на самом деле
какой-то смысл.
(См. статью [4] в нашем журнале про парадокс ЭПР).
В конце концов, квантовая механика - это некая математическая теория, вдруг
она неполна?
Тогда, казалось бы, могла бы быть развита её более изысканная версия, дающая
более рациональное объяснение парадоксальным корреляциям на огромных расстояниях.
Оказывается, что гипотезы о неполноте
квантовой механики - т.е. о наличии каких-то скрытых параметров - действительно могут быть проверены.
И, как ни удивительно, ни одна из таких гипотез не оправдалась.
Когда Аля и Боря выполняют одновременные измерения своих
фотонов, они наблюдают сильные корреляции между результатами измерений.
Поскольку измерения пространственно разделены, эти
корреляции не могут быть следствием обычного обмена сигналами между фотонами,
так как сигнал не может распространяться быстрее, чем свет.
Однако, можно вообразить, что поведение фотонов коррелирует
потому, что они взаимодействовали в прошлом. В конце концов они оба были излучены одним
источником, где они могли бы согласовать общую "стратегию".
Существование некоего скрытого параметра означало бы справедливость концепции "локального
реализма".
В этом случае ещё до измерения квантовый объект можно было бы охарактеризовать определенным значением
некоторой физической величины, например, проекцией момента импульса на фиксированную ось.
Уже давно Белл [5] показал, что в теории с любыми скрытыми параметрами, но в которой есть
только классическая локальность, между вероятностями различных исходов опыта существуют соотношения,
так называемые неравенства Белла.
Если рассчитать вероятности различных исходов опыта по законам квантовой механики, то
неравенства Белла оказываются нарушенными.
До сих пор все лабораторные эксперименты
дали нарушения неравенств Белла, таким образом,
подтверждается квантовая нелокальность [6].
Следовательно, неверным оказывается привычное представление о том, что
динамические свойства квантовой частицы, наблюдаемые при измерении, реально существуют еще до измерения, а
измерение лишь ликвидирует наше незнание того, какое именно свойство имеет место.
На самом деле это не так: свойства, обнаруженные при измерении, могут вообще не существовать до измерения.
В ноябре 2010 г. появилась статья Шайдла и др. [7], описывающая опыты, проведённые в июне-июле 2008 г. на
Канарских островах Ла-Пальма и Тенерифе, расстояние между которыми составляет 144 км.
На Ла-Пальме генерировалась
пара запутанных фотонов, один из которых затем передавался по свёрнутому в кольцо световоду длиной 6 км на
детектор Alice, расположенный рядом с
источником (задержка 29,6 мкс), а другой передавался по воздуху на детектор Bob, расположенный на
Тенерифе (задержка 479 мкс).
Эти 479 световых мкс и есть 144 км.
Конечно, здесь расстояние между Алей и Борей сильно меньше, чем несколько световых лет, упомянутых выше, но суть
от этого не меняется.
Эспериментаторам удалось закрыть лазейки для локального
реализма и свободы выбора во всех системах координат.
Tермин steering
обозначает регулирование (управление) тем, на какой объект ЭПР эксперимента перенести квантовую особенность,
связанную с запутанностью.
Концепция управления предлагает свежий взгляд на квантовые корреляции.
Оригинальный идея восходит к Эрвину Шрёдингеру [2], но она
была надлежащим образом формализована лишь недавно.
Чтобы понять это, давайте
вернемся к нашим двум экспериментаторам
и предположим, что они играют в игру.
Аля, которая имеет источник фотонов, пытается
убедить скептического Борю, что они имеют дело с
запутанным состоянием: она утверждает, что после отправки
фотона Боре, она может "управлять" (to steer) его состоянием
на расстоянии. Действительно, если фотоны
на самом деле запутанны, то квантовая механика
предсказывает, что, выполняя различные
измерений своего фотона, Аля может
удаленно приготовить различные состояния для Бориного
фотона. Приготовленное состояние зависит,
однако, от (случайных) результатов её измерений, и она не может сообщить
о результате быстрее, чем со скоростью света. Но как же убедить Борю, что Аля не обманывает,
например, посылая ему некоррелированный фотон и
только притворяется, что она реально провела измерения на своем фотоне?
Основываясь на своей предыдущей работе, Саундерс и др. [1]
нашли изящное решение этой проблемы.
В 2007 году авторы статьи [1] ввели ассиметричную схему ЭПР экспериментов,
согласно которой можно
описывать измерения в одном из двух каналов классическими вероятностями, удовлетворяющими локальности,
а во втором - квантовыми, которые учитывают ограничения соотношений неопределенности.
Из этих вероятностей строится совместная
вероятность парных измерений (произведение с интегрированием по скрытому параметру).
Они разработали простые "неравенства управления" -
аналогично неравенствам Белла, которые позволяют
Боре определить, действительно ли произошло управление состоянием его фотона.
Сначала Боря просит Алю провести
одно из нескольких возможных измерений на ее
фотоне и сообщить ему результат. Затем Боря измеряет свой фотон, чтобы проверить,
что он имеет правильное состояние. Повторяя эту
процедуру достаточное число раз, Боря может оценить корреляции между
фотонами и проверить неравенство управления.
Неравенство всегда должно выполняться
для любой стратегии обмана, какую только Аля ни придумает, а нарушение
неравенства управления доказывает, что Аля на самом деле приготовила
запутанное состояние.
Не являются ли эти эксперименты всего лишь вариантами тестов Белла?
Это не так. Оказывается, что не все запутанные состояния можно
использовать для управления, и не все управляемые
состояния могут приводить к нарушению
неравенств Белла. Таким образом, управление представляет собой
принципиально новую форму квантовой нелокальности, промежуточную между
запутанностью и нелокальностью (см. рис. 1). Это
именно то, что Саундерс и др. [1] показали на опыте.
Оригинальность их
работы, по сравнению с предыдущими исследованиями,
состоит в прямой демонстрации управления и его
отношения к нелокальности.
В своих экспериментах Саундерс и др. [1] генерируют пару
фотонов, запутанных по поляризации, которые могут быть впоследствии
деполяризованы очень точно.
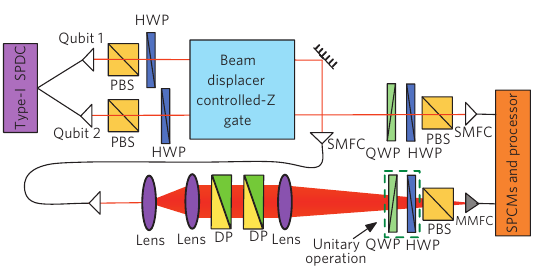
Рис. 3. (Для специалистов). Experimental set-up. Pairs of identical photons are produced
using type-I single photons through spontaneous parametric downconversion
(SPDC) and directed, by single-mode fibres, to a linear-optics
controlled-Z logic gate. After the gate, qubit 1 passes through a pair of
Hanle wedge DPs. By varying the azimuthal angle between the optical axes
of the DPs, we control the amount of depolarizing noise, which sets μ.
Abbreviations: SMFC, single-mode fibre coupler; MMFC, multi-mode fibre coupler.
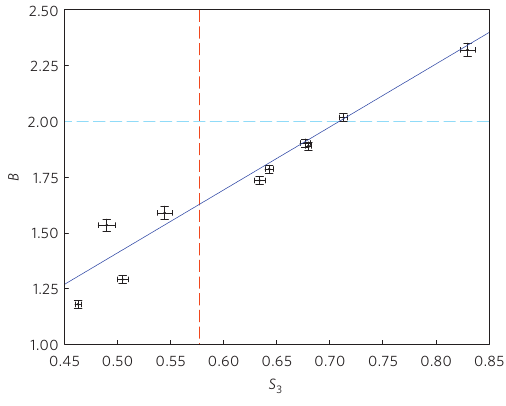
Рис. 4. Экспериментальная демонстрация ЭПР-управления "локальными по Беллу" состояниями.
Горизонтальная штриховая линия - это предел неравенства Белла, а
вертикальная - предел неравенства ЭПР-управления.
Диагональная синяя линия показывает предсказанные значения для вернеровских состояний [8]. Каждая точка
соответствует различным экспериментально произведённым состояниям Вернера. Интервалы ошибок представляют собой
одно стандартное отклонение, они рассчитаны по пуассоновской статистике.
При добавлении точно необходимого количество шума, они приготовливают пары фотонов в запутанных
состояниях, которые являются "локальными по Беллу", - это означает, что
такие пары не могут нарушить никакое из неравенств Белла.
Эти состояния называют вернеровскими [8].
После этого авторы показывают, что эти состояния тем не менее управляемы, путем демонстрации
явного нарушения неравенств управления.
Работа Саундерса и др. [1] может открыть двери для возможных приложений шрёдингеровского управления
в квантовых коммуникациях.
Особо интересно было бы видеть, могут ли быть адаптированы существующие протоколы, безопасность которых
опирается на нелокальность (а практическая реализация по-прежнему не достигнута в
современных технологиях), к протоколам на основе эффекта управления.
Поскольку управление представляет собой более слабую форму квантовой нелокальности, такие протоколы
могут быть проще реализованы на практике и могут привести к новому
поколению в квантовой связи. Время покажет. Пока нам остается размышлять
над новым зачаровывающим аспектом квантовой нелокальности.
По материалам:
N. Brunner Nature physics | VOL 6, p. 842 | NOVEMBER 2010 | www.nature.com/naturephysics
[1] Saunders, D.J., Jones, S.J., Wiseman, H.M. & Pryde, G.J.,
Nature Phys. 6, 845–849 (2010).
[2] Schrödinger, E., Proc. Camb. Phil. Soc. 31, 555–563 (1935).
[3] Einstein, A., Podolsky, B. & Rosen, N., Phys. Rev.
47, 777–780 (1935).
[4] Наумов В.В. Эксперимент Эйнштейна-Подольского-Розена для частиц со спином 1/2 (2011)
[5] Bell, J., Physics 1, 195–200 (1964).
[6] Aspect, A., Nature 446, 866–867 (2007).
[8] Werner, R. F. Quantum states with Einstein–Podolsky–Rosen correlations
admitting a hidden-variable model. Phys. Rev. A 40, 4277–4281 (1989).
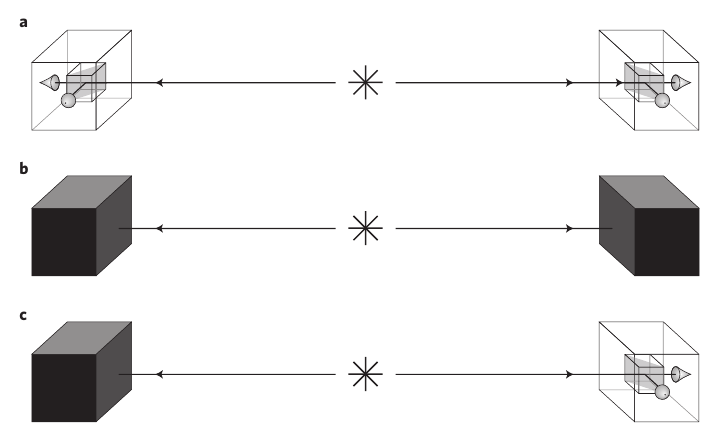
Рис.1. Три принципиально различные формы квантовой нелокальности. a Для проверки
запутанности используются устройства (белые ящики), которые заведомо подчиняются законам квантовой механики.
b Однако, нелокальность определяется независимо от квантовой механики, и может быть проверена без каких-
либо предварительных знаний об устройствах (черные ящики).
c Шрёдингеровское управление является промежуточным: одна сторона доверяет только собственному
измерительному прибору, но не другой стороне.
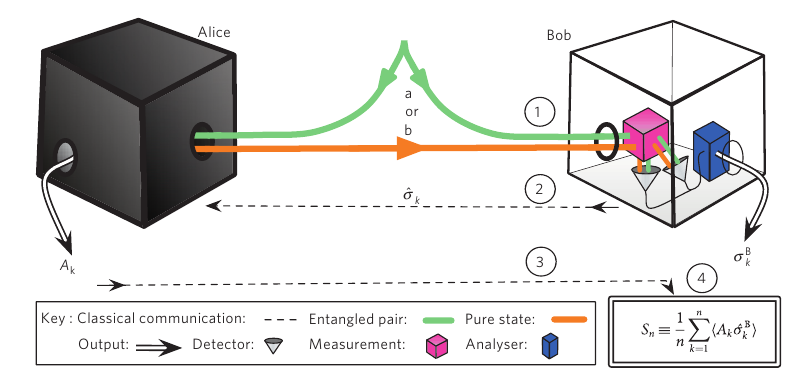
Рис.2. Боря (Bob) сомневается, что Аля (Alice) может удалённо влиять, т.е. управлять (steer)
его состоянием. Боря доверяет своему квантовому прибору (белый ящик), но он не делает никаких допущений о
поведении Алиной системы и её приборов (чёрный ящик).
В опыте 4 этапа. (1) Боря получает свой кубит. Он не знает, получил ли он (a) половину запутанного состояния пары
или (b) чистое состояние, посланное Алей.
(2) Затем он объявляет Але свой выбор измерения из набора {σBk}
(3) Боря регистрирует результат своего измерения σBk и получает ответ Ak,
объявленный Алей.
(4) Боря объединяет результаты и вычисляет параметр управления Sn (после многократного повтора серий
измерений). Если значение Sn больше, чем определенный предел, то Аля доказала, что она
осуществляет ЭПР-управление состоянием Бори, и, таким образом, Боря может быть уверен, что он получил a, не b.