24.04.2003

Перевод статьи Яна Стюарта (Ian Stewart) "The missing link..." New Scientist, vol 176, issue 2368 - 09 November 2002, page 30. http://www.incunabula.org/blog/articles/stewart.html

1,2,4,8,... Что дальше? Ничего. Если разговор о числах, 16 является очевидным следующим членом. Но если подразумевается алгебра определенного типа, следующего члена не существует. И оказывается, что это очень важно. Последнее число, скромная восьмерка, лежит в сердцевине математической системы, известной как октонионы. И эта система похоже является ключом, который позволит физикам соединить вместе квантовую теорию и гравитацию. Как ни странно не звучит, число 8 может привести нас к "Теории Всего".

История октонионов начинается в середине 16-го века. До того времени математики думали, что числа даны Богом раз и навсегда. Никто бы не стал обдумывать изобретение нового числа. Но около 1550г. Итальянские алгебраисты Гироламо Кардано и Рафаель Бомбелли сделали как раз это, написав квадратный корень из -1. Потребовалось около 400 лет, чтобы разобраться, что означала эта штука, но всего 300 чтобы убедить математиков в том, что она слишком полезна для того, чтобы ее просто игнорировать.

Около 1800г., изобретение Кардано и Бомбелли выкристаллизовалось в новый тип числа, i, квадрат которого равен -1. Квадрат "действительного числа", числа знакомых всем нам обычного типа, всегда положителен. Следовательно, что бы то не было i, оно не действительное число, и математики назвали его "мнимым" чтобы подчеркнуть это. Про комбинацию действительного и мнимого числа, как например 4+5i, говорят что она "комплексное число".

Мы живем в интересном мире где, как незабываемо отметил физик Юджин Вигнер, математика "непостижимо эффективна". Комплексные числа могут показаться странными, но они оказываются волшебным средством для понимания физики. Проблемы тепла, света, звука, колебании, упругости, гравитации, магнетизма, электричества и течения жидкости, все уступают этому комплексному оружию, но только для физики в двух измерениях.

Наша Вселенная, однако, имеет три пространственных измерения, если не больше. Следовательно, раз двухмерная система комплексных чисел так эффективна для двухмерной физики, может ли существовать аналогичная трехмерная числовая система, которую можно использовать для физики реального мира?

Нас ждет отрицательный ответ. Ирландский математик Виллиам Рован Гамильтон потратил годы на поиски трехмерной числовой системы, но все без результата. Наконец, 16 Октября 1843 его осенила догадка: не искать в трех измерениях, а искать в четырех. И она сработала. Гамильтон назвал свои новые числа "кватернионами".

Через два месяцев, услышав от Гамильтона про кватернионы, Джон Грейвс, Британский математик и старый друг Гамильтона еще со времен колледжа, объявил что он нашел восьмимерную числовую систему. Он назвал их "октавами". Но до того как Грейвс опубликовал свои результаты, Британский адвокат-математик Артур Кэли сделал то-же самое открытие, и опубликовал его как приложение к ужасной в остальных отношениях работе об эллиптических функциях. Он назвал систему "октонионами".

Открытие октонионов с тех времен приписывается не тому человеку (они часто известны как числа Кэли, даже сегодня). Но на самом деле это не имело большого значения, так как все равно никто не обратил какого нибудь внимания на новые числа. Казалось, что октонионы не более чем причуда Викторианской математики.

Грейвс, однако, не терял энтузиазма и был долго убежден, что его метод перехода от 4 к 8 можно и дальше использовать, получая алгебры размерности 16,32,64 и т.д., для любой степени двойки. Он назвал свою 16-мерную алгебру "седенионами", но не нашел способа сделать ее, также как все остальные алгебры, работоспособной и начал сомневаться в их существовании.

Его подозрения имели основания. Мы сейчас знаем, что эти четыре алгебры, размерности 1,2,4 и 8, единственные, которые отдаленно напоминают обычные действительные числа. Причина в том что, при увеличении размерности, эти системы удовлетворяют все меньшему и меньшему числу алгебраических законов - алгебраическая структура становится беднее. Если говорить несколько упрощенно, на седенионах Грейвса, алгебраическая структура уже в значительной степени пропадает.

Действительные числа, комплексные числа, кватернионы, октонионы; размерности 1,2,4 и 8: это странный набор инструментов, даже по математическим меркам. Эти четыре числовые системы имеют несколько общих черт, то что они "алгебры с делением" -- наиболее удивительная черта. Для многих числовых систем операции сложения, вычитания и умножения хорошо определены: например, когда эти действия применяем к целым числам (...,-2,-1,0,1,2,2,...), они преобразовывают два целых числа в другое целое число. Но тоже самое не скажешь про деление: при делении одного целого на другое часто получается не целое число. Но в упомянутых четырех числовых системах деление всегда возможно и не выводит за рамки той же самой системы.

И это не единственная математическая операция которая выделяет их. Числа этих систем единственные которые имеют "норму", аналог квадрата расстояния комплексного числа от начала: для x+iy комплексного числа нормой является x²+y². Из за существования нормы и возможности деления, эти числовые системы известны как "нормированные алгебры с делением".

Это все очень изящно, по крайнее мере для математика. Но, несомненно, единственные действительно важные случаи - это реальные и комплексные числа. Хорошо, не совсем так: кватернионы тоже показали свою полезность в нескольких эзотерических исследованиях, в таких областях как абстрактная алгебра и топология.

Но несомненная истина состоит в том, что октонионы оставались в тени долгое время. В 1925 Вигнер, работая вместе с математиком Джоном Фон Нейманом, попытался сделать октонионы основой квантовой механики. Но он потерпел неудачу, и октонионы снова канули в мрак. До сегодняшнего дня, то есть.

Несколько удивительно, октонионы оказались самой важной системой из всех. Это потому, что они имеют решающее значение для теории струн, наилучшего кандидата физической Теории Всего. После 150 лет, физика наконец говорит нам в чем предназначение октонионов: они важны для пространства и времени.

Теория струн представляет собой попытку поженить крупномасштабную геометрию Эйнштейновской обшей теории относительности с мелкомасштабной неопределенностью, характерной для квантовой теории. Обе эти теории блестяще успешны в своих областях. Но их нельзя объединить: они эффективно противоречат друг другу при попытке их объединения в рамках одной модели. Поэтому происходил поиск объединяющей теории, которая модифицирует их достаточно, чтобы можно было последовательно объединить, не нарушая при этом их существующий успех.

Нынешним фаворитом этих исследовании и является теория струн. Очень грубо, традиционная идея, что фундаментальная частица представляет собой точечный объект без размеров, отвергается. Вместо этого частицы моделируются как крошечные петли энергии -- вышеупомянутые струны. Эти петли могут разнообразно вибрировать, что приводит к появлению квантовых чисел, типа спина, заряда и очарования.

Но все это работает только если петли многомерные и их поверхность выпадает за пределы обычного четырехмерного пространства-времени. Один из обжигающих вопросов: сколько же тогда на самом деле этих измерении? На данный момент, ответ кажется зависит от нахождения такого числа размерностей для которого теории работают элегантнее всего. И, несмотря на то, что физики еще не имеют окончательного ответа, они заметили что нечто приятное происходит когда они работают в размерностях 3,4,6 и 10. Интересно, что каждое из этих чисел на 2 больше чем размерности соответствующих нормированных алгебр с делением: отнимите 2 из 3,4,6 и 10 и вы получите 1,2,4 и 8. И это не простое совпадение: эти алгебры являются жизненно важной частью теории.

Рассмотрим, например, взаимоотношение между двумя математическими объектами: векторами и спинорами. Вектор, собственно, является просто способом описать нечто имеющее как величину так и направление. Скорость, например, есть вектор, так как он описывает быстроту и направление движения тела. Спинор более эзотерическая математическая новинка, изобретенная Пол Дираком для описания спина электрона. Оказывается, что между векторами и спинорами существует определенное соотношение, справедливое только для пространства-времени размерности 3,4,6 и 10. Это случается потому, что в теории струн размерности 3,4,6 и 10, каждый спинор можно представить двумя числами из соответствующей алгебры, имеющей норму и деление. Это не происходит для любого другого числа размерностей, и отсюда следует много приятных следствий для физики.

Итак мы имеем четырех кандидатов теории струн: действительную, комплексную, кватернионную и октонионную. Из них считается, что больше всего шансов соответствовать реальности имеет 10-мерная теория, так как она искусно обходит ряд математических препятствии, оставляя при этом место для содержательной физики. И в этой системе соотношения между свойствами материи задаются октонионами: если эта конкретная теория и вправду соответствует реальности, тогда наша Вселенная построена из октонионных пар.

Даже если окажется, что 10 измерении не совсем хватает, кажется октонионы все равно будут играть ключевую роль в Теории Всего. Другой очень модный кандидат теории струн, "M-теория", включает в себя 11-мерное пространство-время. Хотя это означает, что соотношение между векторами и спинорами не будет иметь места, зато нечто почти столь же хорошее будет работь. В M-теории нет необходимости слишком скручивать дополнительные измерения, так что ограничение на число дополнительных измерении шестью ослабевает и допускается седьмое дополнительное измерение, только опять без октонионов это не работает.

Чтобы уменьшить размерность воспринимаемой части пространства-времени от 11 до привычных четырех (три пространственных и одно временное измерение), нам придется спрятать остальные семь измерении. Для этой цели их искривляют так сильно, что они уже не проявляют себя. И как это достигается? Можно использовать симметрию октонионов.

Идея симметрии - свойство некоторого объекта не меняться при определенных перемещениях - оказалась центральной в физике, особенно в квантовом мире. Все наши теории фундаментальных частиц, и их странных свойств наподобие спина, заряда и очарования, которые принимают целочисленные значения соответствующих квантов, опираются на симметрии. Использование октонионной симметрии в M-теории даже открывает значение одной математической особенности, существование которой всегда сбывало с толка математиков (см. "Восьмеричный путь"). Так что эффективность октонионов здесь вдвойне приятна.

Несмотря на то, что октонионы начинали как математический курьез, и почти полностью игнорировались в течении 150 лет, их время пришло. Они больше не являются Викторианской причудой, а представляют собой драгоценный ключ к возможной Теории Всего. Каким бы устрашающим не выглядела их математика, физики начинают брать на вооружение этот новый инструмент и работать с ним. Работа опубликованная в этом году Джоном Баецом из Калифорнийского университета, вызвала оживленную Web-дискуссию среды струнных теоретиков. Все сводится к осознанию необычного факта: скромное число 8 больше не является просто числом. Оно - наш ключ к Вселенной.

Восьмеричный путь.

Наш наилучший кандидат для Теории Всего есть теория струн. Эта идея подразумевает, что фундаментальные частицы - это петли энергии, которые существуют в значительно большем числе измерений, чем те четыре, которых мы ощущаем. Многомерные петли могут иметь, в принципе, разнообразные формы. Большая задача для физиков найти правильную форму.

В теории струн, также как в старомодной квантовой теории, симметрия ключевый принцип для определения правильной теории. Физики часто выбирают определенную форму как правильное описание чего-нибудь потому, что она имеет правильную симметрию: похоже Вселенная любит симметричные характеристики. И в теории струн, оказывается, симметрия октонионов имеет решающее значение.

Симметрия какого-нибудь объекта, это его свойство оставаться неизменным при некоторых преобразованиях. Если возьмете однородный круглый диск, например, и повернете его на любой угол, он не изменится. Это пример непрерывной симметрии. Но для квадрата, только повороты на 90 градусов не изменят его.

Окружности и квадраты - не единственные объекты, к которым можно применять операции симметрии. Как не было трудно это представить, алгебры тоже имееют симметрию. Совокупность всех симметрии данной фигуры, алгебры или чего бы то не было, называется ее группой симметрии. В 19-ом столетии, Норвежский математик Софус Ли научился исследовать такие симметрии с помощью алгебраической структуры, известной сегодня под именем группы Ли. Примером является множество вращении объекта в трехмерном пространстве.

Группы Ли, фундаментальные разновидности симметрии, можно поделить на четыре главных семейства. Например, одно семейство составляют группа вращения в плоскости, группа вращения в трехмерном пространстве, группа вращения в четырехмерном пространстве и так далее. Каждая размерность пространства соответствует одному элементу семейства. Другое семейство описывает все возможные способы искажения n-мерного пространства так, чтобы прямые линии оставались прямыми. Снова, для каждой размерности существует одна такая группа. Они представляют собой "линейные отображения" и делают вещи подобные следующим (в случае n=2): растянуть плоскость в направлении север-юг, оставляя при этом направление восток-запад неизменным; или наклонить ось север-юг на 45 градусов не трогая оси восток-запад. Как будто кто-то прислонился к вертикальной оси и надавил на нее. Подобная ситуация и в размерности n>2.

Но существуют пять любопытных групп симметрии, которые не входят ни в одну из семейств. Само существование этих "исключительных" групп, имена которых G2,F4,E6,E7 и E8, представляет загадку и головную боль для математиков, которые любят все упорядочивать. Один отчаявшейся математик даже назвал их "жестоким актом Провидения".

В течении десятилетий, никто не мог найти какое-нибудь применение для исключительных групп, или какую-нибудь причину их существования, и было соблазнительным просто игнорировать их. Но сейчас было осознанно, что все пять из них можно обьяснить в терминах октонионов. На самом деле они составляют свое маленькое семейство, только с пятью членами. И дело выглядит так, как будто октонионы действительно связывают вместе те вещи, которые имеют отношение к Теории Всего.

Чтобы 11 размерностей M-теории свести к четырем, которых мы ощущаем, физикам требуется произвести определенное математическое преобразование над пространством-времени. Единственный способ сделать это требует применения исключительной группы Ли G2. И чем еще является эта героическая группа, которая спасает жизненно важную для физики теорию? Она является группой симметрии октонионной алгебры!

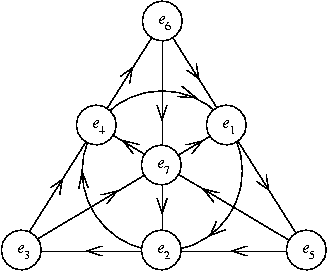
Октонионы имеют восемь единичных элементов: обычную действительную единицу и семь других, которые называются e1,e2, и так далее до e7. Квадрат каждого из них есть -1. Таблица умножения октонионных единиц задается с помощью "плоскости Фано" (см. рис.). Предположим вам надо перемножить е3 и e7, к слову. Найдите на диаграмме соответствующие точки, найдите линию, которая соединяет их, и увидите что на этой линии есть и третья точка, e1. Согласно стрелкам, вы переходите от е3 к e7 и потом к e1. Следовательно, e3*e7=e1. Если порядок следования противоположный, добавте минус знак: e7*e3=-e1. Еще одна вещь, считается что все линии возвращаются к своим началам, так что e1*e3=e7 и e3*e1=-e7. Сделайте это упражнение для всех возможных пар октонионных единиц и будете знать как перемножить октонионы.

Перевел З.К. Силагадзе

Примечания:

1. Про октонионы (элементарное введение) можно прочитать в книге:
И.Л. Кантор, А.С.Солодовников. Гиперкомплексные числа. М., "Наука", 1973.

2. "В 1925 Вигнер, работая вместе с математиком Джоном Фон Нейманом, попытался сделать октонионы основой квантовой механики" - по видимому имеется в виду работа:
P.Jordan, J.von Neumann and E.P.Wigner, On An Algebraic Generalization Of The Quantum Mechanical Formalism, Annals of Mathematics 35 (1934) , 29. Для более современной попытки использовать октонионы в квантовой механике, смотрите:
M.Gunaydin, Moufang Plane And Octonionic Quantum Mechanics, http://ccdb3fs.kek.jp/cgi-bin/img_index?7806065

3. Хорошая обзорная статья по алгебрам Иордана:
K. McCrimmon, Jordan algebras and their applications, Bull. Amer. Math. Soc. 84 (1978), 612.

4. Про теории струн, без формул, можно прочитать здесь:
E.Witten, Comments on string theory, http://arXiv.org/abs/hep-th/0212247 Более техническое, но все еще элементарное введение:
D.I. Olive, Introduction to String Theory: Its Structure and its uses, Phil. Trans. Roy. Soc. Lond. A 329 (1989), 319.

5. Упомянутую работу Баеца (J.C. Baez, The Octonions, Bull. Amer. Math. Soc. 39 (2002), 145) удобно читать здесь:
http://www.math.ucr.edu/home/baez/Octonions/

6. Связь между исключительными группами Ли и октонионами: Г. Фрейделталь, Октавы, особые группы и октавная геометрия, Математика 1 (1957), 117.
P.Ramond, Introduction To Exceptional Lie Groups And Algebras, http://ccdb3fs.kek.jp/cgi-bin/img_index?197703037 Обзорная статья:
J. R. Faulkner and J. C. Ferrar, Exceptional Lie algebras and related algebraic and geometric structures, Bull. London Math. Soc. 9 (1977), 1.
Смотрите еще лекции
R.S. Garibaldi, Exceptional algebraic groups, http://www.mathcs.emory.edu/~skip/classes/eag/eag.html

7. Попытка популярно объяснить роль группы G2 в теории струн: http://www.math.ucr.edu/home/baez/week195.html M-теория и октонионы:
L. J. Boya, Octonions and M-theory, http://arXiv.org/abs/hep-th/0301037 P. Ramond, Exceptional Groups and Physics, http://arXiv.org/abs/hep-th/0301050

8. Спиноры ввел в математику Эли Картан. Смотрите его книгу:
Э. Картан, Теория спиноров. Из серии "Шедевры мировой физико - математической литературы", изд-во "ИО НФМИ", 1998. Спиноры в n-мерном пространсве:
R. Brauer and H. Weyl, Spinors in n dimensions, Amer. J. Math. 57 (1935), 447.

9. Соотношение между векторами и спинорами особенно интересно в восьмимерном пространстве:
A. Gamba, Peculiarities of the Eight-Dimensional Space, J. Math. Phys. 8 (1967), 775.

Обсудить на форуме