О том, что физики в последние годы "открыли" в привычном нам мире
дополнительные пространственные измерения
— "в нагрузку" к высоте, длине и ширине —
слышали не только специалисты, но и люди, интересующиеся
наукой постольку-поскольку (для введения в предмет читайте заметку
Трехмерен ли наш мир?).
Однако среди потока работ, посвященных свойствам
мира с дополнительными пространственными измерениями,
особняком стоит недавняя статья [ Попытаемся пояснить суть дела.
Начнем с формального построения, предложенного в статье.
Рассмотрим мир с тремя пространственными и одним временным измерением,
в котором существует не привычные нам
сильное, слабое и электромагнитное взаимодействия
(гравитацию пока оставим в стороне), а целый набор
различных взаимодействий. А именно, пусть у нас будет
N штук различных по своей природе взаимодействий,
которые, тем не менее, математически похожи друг на друга
(а именно, они описывается одной и той же группой калибровочной
симметрии G; для конкретности авторы рассматривают группы SU(m)).
Кроме того, пусть у нас существует и вещество
— N штук "адронных" полей, причем каждое поле
чувствует не все возможные типы взаимодействий, а только два
(некий аналог: электроны, которые чувствуют
электромагнитное и слабое взаимодействие, но не чувствуют сильного).
В результате возникает "кольцевая диаграмма" теории,
проиллюстрированная на Рисунке: N узлов диаграммы — это
взаимодействия; N соединяющих их линий — это "адроны".
Оказывается, что эффективное действие (скалярный функционал,
описывающий весь мир) в такой теории имеет интересную особенность:
кроме обычного интеграла по 4 пространственно-временным измерениям
имеется еще и суммирование по номеру взаимодействия от 1 до N.
Именно на это суммирование авторы и обратили внимание.
Они указывают на то, что именно такое эффективное действие
возникает в пятимерных моделях (4 пространственных измерения
плюс время), в которых одно пространственное измерение не непрерывно,
а дискретно, что автоматически превращает интеграл в сумму.
Далее авторы задаются вопросом: насколько аналогия суммированием
по типам взаимодействий и суммированием по дополнительной координате
полезна и корректна? Развивая свои идеи, авторы находят подтверждения
тому, что эта дополнительная степень свободы в самом деле
может с полным правом называться еще одним пространственным
измерением. В частности, в пределе N стремится к бесконечности
новая координата становится непрерывной.
При этом в конструкции возникает полная вращательная симметрия между
всеми четырьмя пространственными измерениями.
Например, связь энергии частицы с импульсом имеет вид
E2 = p2 + p52,
где p есть обычный трехмерный импульс, а p5 —
некий квазиимпульс, естественным образом появляющийся в задаче
(полный аналог того квазиимпульса, который возникает
при квантово-механическом рассмотрении N потенциальных ям, свернутых
в кольцо, как показано на Рисунке).
Кроме того, если рассмотреть потенциал между двумя частицами как
функцию расстояния, то он в этой модели принимает вид 1/r2
(а не 1/r, как в трехмерном мире), что также говорит о реальности,
физичности нового измерения.
Итак, аккуратно сформулируем физическую идею находки.
Дополнительные пространственные измерения не обязательно
вводить в теорию руками, как это делалось до сих пор.
Как показано в этой статье, они, в принципе,
могут получаться динамически. Разумеется, для этого требуется
определенный, достаточно экзотический набор физических полей
и взаимодействий, которого, по-видимому, нет в нашем конкретном мире.
Тем не менее, говорить, что эти идеи к нашему миру не имеют никакого
отношения, пока преждевременно. В самом деле, а вдруг окажется,
что одно (несколько? все?) из наших привычных пространственных
измерений "сгенерированы" вот таким же образом, динамически,
на каком-нибудь глубоком и пока нам недоступном уровне?!
Как именно эти идеи можно применить к нашему миру, покажет будущее.
Однако стоит отметить, что статья действительно привносит
совершенно свежую струю идей в гипотезу дополнительных пространственных
измерений.
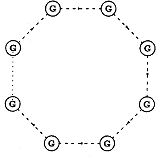
Схематическая структура мира в рассматриваемой модели:
имеется N калибровочных полей и N полей вещества, чувствительных
только к паре взаимодействий.