Нелокальность – фундаментальная особенность квантовой механики. Она
проявляется в наличии неклассических корреляций между пространственно удаленными друг от друга
частями одной квантовой системы. Для экспериментальной демонстрации нелокального характера этих
корреляций обычно используют так называемые ЭПР-пары (Эйнштейн, Подольский, Розен) из двух
частиц, находящихся в запутанном состоянии. Как правило, такие эксперименты проводят с фотонами.
Между тем в любом твердом теле имеется огромное количество самых что ни на есть квантовых
объектов – электронов, которые тоже могут образовывать перепутанные ЭПР-пары. Но все эти
электроны находятся в макроскопическом основном состоянии ("фермиевском море"), из которого
нельзя просто так выделить два электрона, запутанных только между собой. Однако есть исключение:
любой сверхпроводник может служить источником ЭПР-пар электронов – куперовских пар в синглетном
состоянии. Отдельные куперовские пары можно извлечь из сверхпроводника за счет их туннелирования
через барьер, но для изучения квантовых корреляций нужно еще научиться расщеплять такие пары на
отдельные электроны контролируемым образом. Для решения этой задачи в работе был использован
Y-образный контакт (см. рис. 1), каждое металлическое плечо которого включало квантовую точку с
регулируемым энергетическим уровнем. Большие энергии зарядки квантовых точек (2 - 4 мэВ)
препятствовали туннелированию через них куперовской пары как целого, а процессы последовательного
туннелирования обоих электронов пары через одну квантовую точку были подавлены за счет
сравнительно толстых туннельных барьеров. О наличии нелокальных корреляций между двумя
протуннелировавшими электронами ученые судили на основании синхронного измерения туннельных
проводимостей двух контактов. При температуре, превышающей критическую температуру
Tc, эти корреляции отсутствовали. Эффективность такого "генератора" запутанных
электронов составила около 2%, на много порядков больше, чем при генерации запутанных фотонов
(10-12). В принципе, "делитель куперовских пар" можно использовать в твердотельных
квантовых вычислительных устройствах.
Источник информации - заметка Л.Опенова в бюллетене
ПерсТ, выпуск 20 за 2009 г.
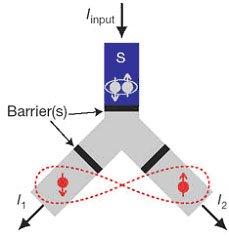
Рис.1.Схематическое изображение эксперимента. Проходя через Y-образный контакт,
куперовская пара расщепляется на два пространственно разделенных (но остающихся в запутанном
состоянии) электрона/